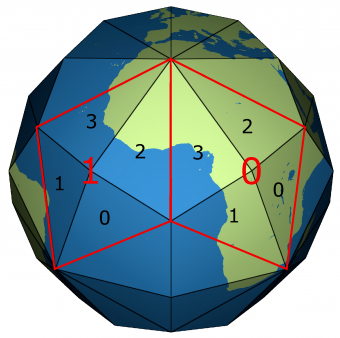
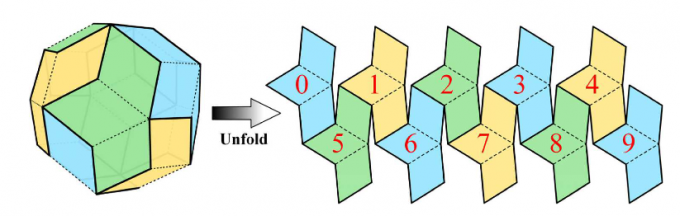
Proyección sobre un poliedro de 120 caras, del inglés Disdyakis Triacontahedron (es un sólido catalán con 120 caras triangulares idénticas), propuesta en 2020 por https://www.mdpi.com/2220-9964/9/5/315
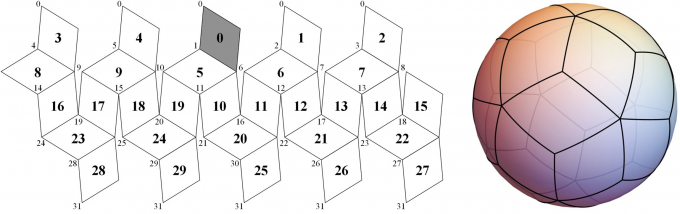
Abajo el poliedro de 120 caras:

Cada una de las 120 caras corresponde a un plano de proyección del tipo "Slice and Dice projection" (van Leeuwen y Strebe).
Proyección Slice and Dice
La proyección de van Leeuwen y Strebe, originalmente orientada a triángulos equiláteros, fue optimizada para menor distorsión angular en triángulos isósceles en el mismo año, https://www.arxiv.org/pdf/2008.13670v1 pero publicada solo en 2021, https://doi.org/10.1145/3460521
La proyección DT hace uso de triángulos isósceles, por lo tanto está pendiente analizar la optimización.
Además del original cerrado, y alguna descripción en los artículos citados, la proyección equivalente en área "Slice and Dice" (van Leeuwen y Strebe) está descrita en https://www.researchgate.net/publication/250016113_A_Slice-and-Dice_Approach_to_Area_Equivalence_in_Polyhedral_Map_Projections (donde podemos pedir al autor).
Modelado del triacontaedro rómbico
La reunión de 4 en 4 caras resulta en un Triacontaedro rómbico de 120/4=30 caras cuadriláteras, usadas como L0 de un GGeohash.
En las caras del wikipedia:Rhombic triacontahedron, el ángulo menor del rombo es de 63.43°, más cercano a 90° que el rombo de la proyección DGGS/Proj/ISEA, por eso superior (con capacidad) también en el formato de la celda.
Trabajos recientes de Liang et al. 2022 reecuacionaron la construcción de los cuadriláteros de la proyección, https://doi.org/10.1080/17538947.2022.2130459
Ajuste local del país
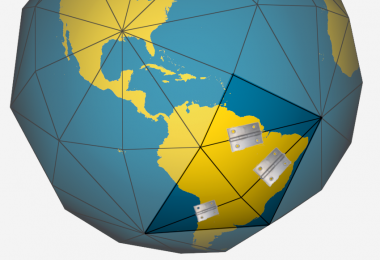
Aún en estudio si realmente es viable... Estrategias complementarias, usando Propuesta de la re-proyección lineal (bisagras), para ajuste al relieve del país, o al menos a su altitud mediana. La estrategia puede hacer uso de:
- Cambio de radio de elipsoide, para que el geoide tangencie mejor la altitud mediana. No es bien visto por causar efectos colaterales indeseados en el posicionamiento.
- Cambio en la elección del "plano secante al elipsoide". Esto permite alguna compatibilidad entre ambos, DGGS y DNGS, por estar usando los mismos polígonos en la proyección (los ángulos sólidos se preservan).
En el uso del DT para cada DNGS (cada país), la elección de los cuadriláteros deja de tener mayor compromiso con el rhombic triacontahedron, es libre. Vuelve a ser el compromiso con el m2 como referencia. La "compatibilidad" entre DNGS y DGGS (basados en proyección DT) estaría solo en el uso de la proyección de referencia y simplicidad en los algoritmos de conversión entre rejillas.
Conversión ISEA
H3 Uber y diversas otras implementaciones del estándar DGGS hicieron uso de la proyección ISEA, que parecía la más adecuada hasta los años 2020. Según Huang et al. 2024, en "Bidirectional mapping between rhombic triacontahedron and icosahedral hexagonal discrete global grid systems",
- El icosaedro es actualmente el poliedro principal en la investigación y aplicación de los sistemas de cuadrícula global discreta (DGGS). Sin embargo, comparado con el triacontaedro rómbico (RT), el icosaedro tiene desventajas, como menor precisión de ajuste a la esfera, mayor distorsión de proyección y dificultad para incorporar la estructura matricial para el almacenamiento de datos geoespaciales.
El artículo demuestra técnicas eficientes de conversión del "legado ISEA" en la proyección DT.
La ilustración abajo muestra cómo el rombo puede servir de referencia para 3 tipos de mosaicos:
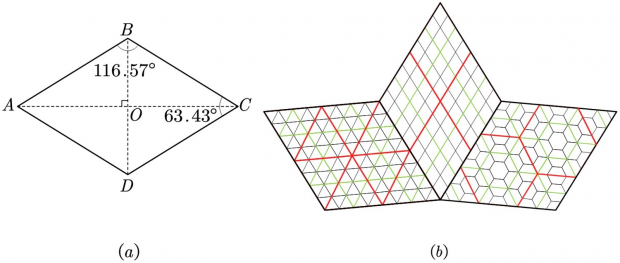
PD: ver también artículo https://doi.org/10.3390/ijgi11120595
Véase también
- DGGS/Proj/ISEA
- Uso en https://www.mdpi.com/2220-9964/11/6/322 para distance transform Canada