DGGS/Proj/DT

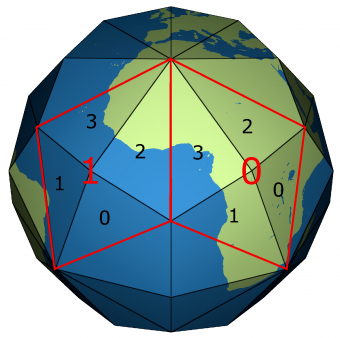
Projection onto a 120-sided polyhedron, from the English Disdyakis Triacontahedron (is a Catalan solid with 120 identical triangular faces), proposed in 2020 by https://www.mdpi.com/2220-9964/9/5/315
Below is the 120-faced polyhedron:

Each of the 120 faces corresponds to a projection plane of the "Slice and Dice projection" type (van Leeuwen and Strebe).
Slice and Dice projection
The van Leeuwen and Strebe projection, originally oriented towards equilateral triangles, was optimized for less angular distortion in isosceles triangles in the same year, https://www.arxiv.org/pdf/2008.13670v1 but published only in 2021, https://doi.org/10.1145/3460521
The DT projection uses isosceles triangles, so optimization is pending analysis.
Besides the original closed, and some description in the cited articles, the equal-area "Slice and Dice" projection (van Leeuwen and Strebe) is described in https://www.researchgate.net/publication/250016113_A_Slice-and-Dice_Approach_to_Area_Equivalence_in_Polyhedral_Map_Projections (where we can request from the author).
Modeling the rhombic triacontahedron
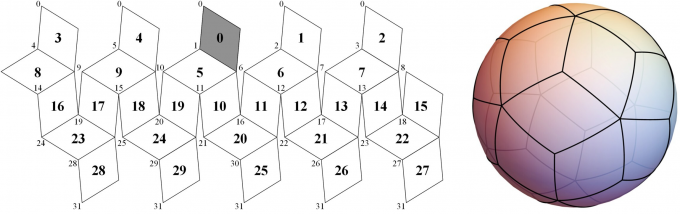
The assembly of 4 by 4 faces results in a Rhombic triacontahedron with 120/4=30 quadrilateral faces, used as L0 of a GGeohash.
On the faces of the wikipedia:Rhombic triacontahedron, the smaller angle of the rhombus is 63.43°, closer to 90° than the rhombus of the DGGS/Proj/ISEA projection, therefore superior (with capacity) also in the cell shape.
Recent works by Liang et al. 2022 re-equated the construction of the quadrilaterals of the projection, https://doi.org/10.1080/17538947.2022.2130459
Local country adjustment
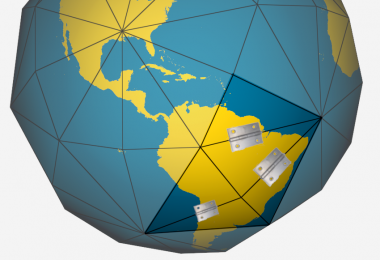
Still under study if truly viable... Complementary strategies, using Proposal of linear re-projection (hinges), for adjustment to the country's terrain, or at least its median altitude. The strategy may utilize:
- Change of ellipsoid radius, so that the geoid better tangents the median altitude. Not well-regarded due to causing undesirable side effects in positioning.
- Change in the choice of the "secant plane to the ellipsoid". This allows some compatibility between the two, DGGS and DNGS, as they use the same polygons in the projection (solid angles are preserved).
In the use of DT for each DNGS (each country), the choice of quadrilaterals no longer has a greater commitment to the rhombic triacontahedron, it is free. The commitment returns to m2 as a reference. The "compatibility" between DNGS and DGGS (based on DT projection) would only be in the use of the reference projection and simplicity in the conversion algorithms between grids.
ISEA Conversion
H3 Uber and several other implementations of the DGGS standard made use of the ISEA projection, which seemed the most suitable until the 2020s. According to Huang et al. 2024, in "Bidirectional mapping between rhombic triacontahedron and icosahedral hexagonal discrete global grid systems",
- The icosahedron is currently the mainstream polyhedron in research and application of discrete global grid systems (DGGS). However, compared to the rhombic triacontahedron (RT), the icosahedron has disadvantages, such as lower sphere-fitting accuracy, greater projection distortion, and difficulty in incorporating the matrix structure for geospatial data storage.
The article demonstrates efficient techniques for converting the "legacy ISEA" in the DT projection.
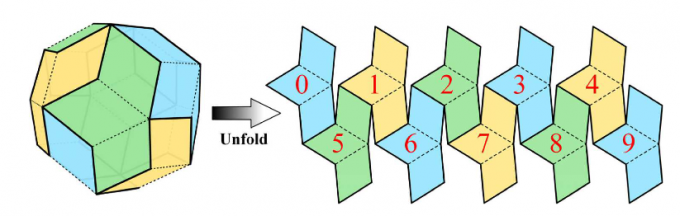
The illustration below shows how the rhombus can serve as a reference for 3 types of tiles:
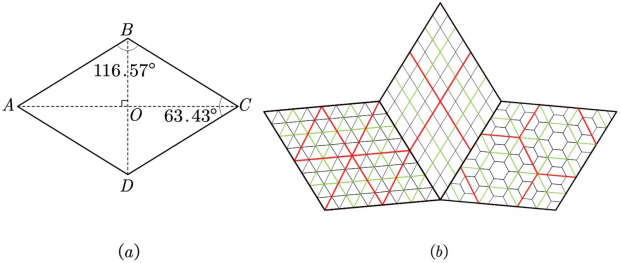
PS: see also article https://doi.org/10.3390/ijgi11120595
See also
- DGGS/Proj/ISEA
- Usage in https://www.mdpi.com/2220-9964/11/6/322 for distance transform Canada