Ref-list/convert/KraEtAll2019
Natural Codes as foundation in hierarchical labeling and extended hexadecimals for variable-length bit strings
Peter Krauss^([1]), Thierry Jean1, Daniele R. Sampaio^([2]), José Damico^([3]), Everton Bortolini1,^([4]), Rui Pedro Julião^([5]), Alexander Zipf ^([6]), Alan C. Alves^([7])
ABSTRACT
We propose a positional notation for bit strings (binary sequences) with an arbitrary amount of bits, which preserves hierarchy and is compatible with the ordinary hexadecimal numeric representation. When the elements of a nested set are labeled with natural numbers, the hierarchical structure is not preserved; but when the numerical labels are replaced by variable-length bit strings, distinguishing leading zeros (00 and 0 as distinct entities), it is possible to express labels with hierarchical syntax, preserving the original nested structure, and classical hexadecimals as subset. We present a formal definition of this type of numerical labeling system, calling it Natural Codes. We also show that it can be transformed into human-readable encodings (positional notations such as base4, base8 or base16), the base notation extensions base4h, base8h and base16h for hierarchical representation. The reference-model adopted is the finite Cantor set with hierarchy degree k — strictly, the set Ck is the “hierarchical tree of the Cantor set”, which is isomorphic to a complete binary tree —, proposing a simple labeling process, mapping elements of Ck into elements of the Natural Codes. The proposal of the base notation extensions introduces a complement to ordinary base syntax, where the last digit can use, when necessary, a complementary alphabet to represent partial values (with one bit less than ordinary digits). The hierarchical representation is a superset, differenciating from ordinary base notation by this last digit, that is a non-hierarchical member of the representation (named nhDigit). We also offer algorithms for implementing the conversion of the base extensions, and we discuss optimizations.
key-words: human-readable encoding, hierarchical labeling, leading zeros, base conversion.
Draft (pre-print) v0.7.2 of Mar 22 '2023
Registered in the Fundação Biblioteca Nacional with protocol number 2801/19
Introduction
We use natural numbers (ℕ) for counting and labeling, but sometimes, to represent hashes, geocodes, or hierarchical indexes, we need a kind of “number” where 0 is not equal to 00, while preserving properties of natural numbers like order (e.g. 011>010) and the freedom to translate its positional notation to some other base (e.g. binary to hexadecimal).
In the set of apples illustrated, each apple was identified by a
variable-length bit string, so the set A of the identifiers is
A = { 0, 00, 000, 01, 010, 011 }.
It’s easy to separate apples from other fruits, because all apple labels starts with “0”. It’s also easy to select green apples, because they have the “01” prefix, G = { 01, 010, 011 } ⊂ A. This characteristic of differentiation through prefix preservation in subsets of labels can be important, and it is only possible to express with bit strings — as we will show, strictly speaking, for infinite sets, it is impossible with only ℕ.
Each element of A can also be interpreted as a binary number. For example, the decimal value of binary 01 is 1, or with base-subscript notation, [01]2=[1]10. Also [010]2=[2]10 and [011]2=[3]10 , but there is some loss of information when adopting equivalence in [0]2 = [00]2 = [000]2 = [0]10. There is a loss of uniqueness of the labels of red apples, all of which have value zero but 1, 2 or 3 bits of size.
A solution to avoid this information loss is to transform each bit
string into a pair of decimal numbers (size,value):
A’ = { (1,0), (2,0), (3,0), (2,1), (3,2), (3,3) }.
Interpreting some samples: the element 0 of A was transformed into (1,0) of A’, it has a size of 1 bit and numeric value zero, [0]10=[0]2; the element 011 was transformed into (3,3), it has a size of 3 and value [3]10=[11]2=[011]2.
Neither the bit strings of A, nor the equivalent pairs of A’ have a specific mathematical designation, but there are many applications that make use of such labels, so we have named them Natural Codes^([8]) (the name “Sized Naturals” was also used in first versions).[]
Examples of real life encoding systems that exhibit such labeling characteristics:
- Two checksums (e.g. CRC32 digests) with different lengths are distinct, we can’t eliminate leading zeros. The CRC32 human-readable standard representation is hexadecimal preserving leading zeros. E.g. 000fa339 is not equal to fa339.
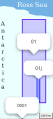
- Two Geohashes with different lengths are distinct, e.g. 01 is a cell identifier of a geographic location little below Ross Sea with ~115000 km², and 0001 is a cell far below, with 3.5 km². There is also a cell 01j inside 01 with ~2700 km². All the illustrated cells have with the same first-digit prefix, they are contained into the bigger 0 cell.
The Geohash encoding system uses base32 as human-readable standard representation, but internally the encode function uses the bit string. - Indexing a binary tree where the left edges are labeled 0 and the right edges are labeled 1: a node is labeled by the concatenated string of branch labels from the root to the node. Example: to reach node 01 from root, take the path of edges labeled 0 and 1.
The purpose of this article is to define Natural Codes and a hexadecimal representation for them.
Indexing hierarchical items with bit strings
In Mathematics, the Cantor set is used as reference model to express concepts like self-similarity and subdivision rule. In Computation, the equivalent reference model is the complete binary tree. We can use either one here as reference for indexing and hierarchical labeling. Let’s use the Cantor Set.
[]
Each element of the “tree of the Cantor set” (red), a “Cantor subset” (black), can be uniquely labeled by a bit string, therefore an identifier (ID), similar to the labelling of the set of apples.[]
Each ID retains information of its left (0) or right (1) positions, as well as its vertical position in the hierarchy of elements — each ID has a prefix that is the ID of its parent. Example: the parent of 011 is 01.
Adopting the convention that set Xk is the set of identifiers of the Cantor subsets limited to k-bits.
X1 = {0, 1};
X2 = {0, 00, 01, 1, 10, 11};
X3 = {0, 00, 000, 001, 01, 010, 011, 1, ..., 111};
Xk = ...;
X8 = {0, 00, 000, 000, ..., 11111110, 11111111}. In usual applications, the set Xk is the domain of a set of identifiers (or indexes), and k is finite.
Example: the set X3 is the domain of the illustrated set A of apples, A⊂X3.
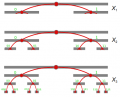
There is an intuitive recursive construction rule (illustrated) for each new Xk after X1 Xk = Pk U Xk-1 where Pk is the set of all of 2k numbers expressed as fixed-length (k) bit strings — and opportune to remember that the elements of Pk can be mapped (casted) to the Naturals of the range 0 to k-1 by its binary representation. Example: X2 = P2 U X1 = {00, 01, 10, 11} U {0, 1}.
The number of elements, |Xk|, after |X1|=2, is the recursion |Xk| = |Xk-1| + 2k. Examples, for k ranging from 2 to 8:
|X2| = 2+4=6; |X3| = 6+8=14; |X4| = 14+16=30; ...; |X8| = 254+256=510.
By induction we see that |Xk| = 2k+1 − 2. As suggested by this power k+1, is possible to map any Natural Code (l,n) to a number n+2l+1, because it preserves n and the leading zeros information.
The hierarchy of the elements of Pk is visible in the illustration above: the last line, that is the subset Pk of new members, has elements x formed by the concatenation (operator ⊕) of prefix p and suffix s, x=p⊕s, where p is the parent identifier and s is the left or right label. Example: the parent 01 of 010=01⊕0 and of 011=01⊕1.
It’s possible to “protect leading zeros” and represent a finite Natural Code by a natural number. Any Natural Code (l,n) can be mapped to a number n+2l without loss of the leading zeros.[]
The illustration shows the Natural codes of k=3, transformed in a set X ’ of Naturals, where the first bit is the value 2l added to n of each original (l,n) element of X3.
This strategy can be used to simplify the internal representation in algorithms and, in some circumstances, as a mathematical alternative to the bit string or ordered pair representations.
In order to “externalize” this internal numeric representation as bit string we must remove the first bit, so we can say that the first bit is “hidden” from the outside of the storage and its algorithms.
In Set Theory (as foundational system), is important to remember that a set of “all bit strings” is isomorphic to a set of Naturals by this transformation, only when the set is finite (or countably infinite) and all its elements are finite. Otherwise, by Cantor's theorem, there cannot exist a one-to-one function from the set of infinite-length bit strings to ℕ.
For finite sets, for example in a computer with 16 bits fixed-length unsigned integer, the conversion is a right-copy. For example for bit string “010” and left-side-hidden-bit concatenation (results “1010”), the internal integer representation will be “0000000000001010”. Operations like “+1” make sense on same set P, will be “1011” in this example. And there is a second way to implement it in fixed-length: as left-copy. In the same 16 bits example the left-copy and right-hidden-bit, for “010”, will result in “0101000000000000”. It loss the consistent integer number representation and its operations (the “+1” results in “0101000000000001”). But it preserves, on bitwise operations, the hierarchical prefix: it is easy and has good performance on hierarchical analysis, see section Algorithms for details.
Empty and inverse elements
A finite set, to be a first-class citizen in Mathematics, must be the generator of a group. Suppose the illustrated G = ( X2 ∪ {∅}, + ).
The introduction of the simbol “∅” as the neutral element of cyclic addition is useful for bit string representation, because “empty string” is a valid value. The unit is the element “0”, to follow the “+0” lexicographical order in this representation system.
Any “x+0” of Xk , when length(x)<k, is a concatenation, like in an unary numeral system. For example “1+0=10”. Otherwise “x+0” is a Turing Machine operation, analysing the last digit of x: when “0” replace it by “1”, else cut “1”s and replace residual “0” by “1”. When cut them all the result is ∅, as “11+0=∅” in the X2 example. The illustrated group G is isomorthic to the quotient group of seven elements, ℤ/7ℤ. It is possible to see also any bit string as a p-adic number with p=2, so it is possible to conceive G as a ring of p-adic integers.
Problem on positional notations
It is not possible, with usual non-binary positional notations like hexadecimal, to represent all Natural Codes. Even the most simple, base4, as illustrated by question marks below.
Table 1 (size,value) BitString Base4 Base16 (1,0) 0 ? ? (2,0) 00 0 ? (3,0) 000 ? ? (4,0) 0000 00 0 (5,0) 00000 ? ? (6,0) 000000 000 ? (7,0) 0000000 ? ? (8,0) 00000000 0000 00 (8,1) 00000001 0001 01 (7,1) 0000001 ? ? (8,2) 00000010 0002 02 (8,3) 00000011 0003 03 (6,1) 000001 001 ? (7,2) 0000010 ? ? (8,4) 00000100 0010 04 (8,5) 00000101 0011 05 ... ... ... ...
The table above shows that the pairs (l,n) of the first column, titled (size,value), can always be represented by a bit string of the second column, and vice-versa, but not always in base4 or base16.
A bit string x can be converted to a base b only when the number of bits x_l of the bit string is a multiple of dpd=ceil(log2(b)), i. e. the number of bits per digit of the base b. Expressing in terms of remainder (modulo operation), it is only possible when x_l % dpd = 0. Examples: in Table-1 the column base4 doesn’t have question marks, “?”, when the size is 2, 4, 6 or any other even size. That’s because when b=4 we need log2(4)=2 bits/digits. The column base16 doesn’t have “?” when the size is 4, 8 or any multiple of 4, because when b=16 we need log2(16)=4 bits.
Testing a naive solution and requirements to the optimal
Seeing how the simplest strategy doesn’t work. A common solution to
preserve leading zeros is to use an external symbol instead of a leading
zero. For example the RFC 4648, section 3.2, suggests:
(...) the use of padding ("=") in base-encoded data (...).
Let's use the letter “Z” as external symbol. Using the illustrated set A of apples to exemplify: A = { 0, 00, 000, 01, 010, 011 } = { 0, Z0, ZZ0, Z1, Z10, Z11 } Can we preserve this external symbol when we translate the set to base4? The natural tanslations are: Z0⇒0; Z1⇒1; 10⇒2; 11⇒3; ZZ⇒Z. For example “ZZZZ10” to “ZZ2” and “ZZ11” to “Z3”.
But what about “0”, “1”, “ZZ0” or “ZZ1”? To translate the bit string representation to its analog base4 string we need to add more external symbols (beyond “Z”), suppose A, B, C, D and E: 0⇒A; Z0⇒C; ZZ0⇒ZA; 01⇒1; Z10⇒DA; Z11⇒DE. This translation results in A’ = { A, C, ZA, 1, DA, DE }. No hierarchy is perceived, and only element “1” ressambles to ordinary base4.
Conclusion: extending base4 alphabet with symbols "Z", "A", ..., "E" does not seem useful. When translating leading zeros from base2, we lost hierarchy visualization. The demand for a lot of new external symbols is also a problem, since human-readability requires something simple that resembles base 4 in most of its representation.
The ideal (optimal) representation is a superset for ordinary base 4 and include a minimal alphabet for the exotic elements: we will show in the next sections that ideal representation exists, by simply adding a new last digit when it’s needed. In the example of set A, we will show that the solution results in A’ = {G, 0, 0G, 1, 1G, 1Q}, where 83% of the elements (5 in 6) resembles ordinary base 4: or translation is exact (“0” from 00⇒0 and “1” from 01⇒1), or preserves hierarchy (commom prefixes has been preserved at “0G”, “1G” and “1Q”).
Objectives
The aim of this document is to define Natural Codes, review its foundations and dedicate to the public domain the algorithms of its representation in the extended positional notations:
- the base4h representation for bit strings of arbitrary length, that is the “ordinary base4 whith leading zeros” when the length of the bit string is even, and an extension of base4 when the length is odd.
- the base8h representation for bit strings of arbitrary length, that is the ordinary base8 when the length is a multiple of 3, and an extension of base8 when it’s not.
- the base16h representation for bit strings of arbitrary length, that is the ordinary base16 (hexadecimal) when the length is a multiple of 4, and an extension of base16 when it’s not.
In the context of software development and programming languages, it’s expected to promote data types (of hashes, geocodes, hierarchical indexes, etc.) to first-class citizens based on Natural Codes.
License
The contents of this article are dedicated to the public domain, in the terms of the CC0 license, “Creative Commons CC0 1.0 Universal”, and its translations, https://creativecommons.org/publicdomain/zero/1.0/legalcode except by the source-code, partial at appendix and complete at git repository, licensed by Apache v2.0.
Formal definition of Natural Codes
The fundamentals of Set Theory are described in Halmos (1960), and the convention for the set of natural numbers (e.g. adopting 0 as element of ℕ) are reinforced in ISO 80000-2:2009. The classic reference-models for the bit string concept are the “strip of tape of bits” of Turing (1937) and the binary message of Shannon (1948). “The set of the Natural Codes” is a particular name for “the set of all bit strings”, and the following is a formal definition oriented towards the introduced labeling applications. The Natural Codes are also indifferent in regards to the element's representation, as bit strings, as ordered pairs of numbers or other.
We can transform all elements of ℕ into bit strings, through the element’s binary representation (base2), forming the set L of labels of ℕ. Still, L is a subset of Natural Codes because bit strings can use leading zeros, representing distinct elements.
The bit-length of a bit string is its number of bits. Otherwise, the standard way to express the "size" of an element of ℕ is through the number of digits in its base2 representation, which is known as the bit-length of the number. To avoid confusion we adopt the "minimum Bit-Length" (minBL) function:
[]
All Natural Codes with bit-length k can be expressed as a set Pk
[]
The finite set Xk of all Natural Codes with maximum bit-length k can be defined by recursion:
[]
Table-1 shows an example, a sample of X8 set. Because of finite size of the real-world fractal structures, the set Xk of labels must be mapped into finite Cantor set, as described by Merlo et al. (2003). In this context, the elements of a set Pk can be used as ordered labels of the Cantor bars of level k.
Terminological note. All the elements of Xk can be mapped to a full hierarchical structure of level k, Ck = {X1, X2, ... , Xk}, the “hierarchical collection of Cantor sets” (see next section). Using analog construction rules, Merlo et al. named it also as “hierarchical tree of the Cantor set”.
Any element of Xk can be expressed as bit string by the function toBitString(l,n), that is the binary representation of n with padding zeros to l. They are semantically equivalent: the bit string and the ordered pair representations.
The hierarchy expressed by the recursion is embedded in both element representation options:
- as a bit string x of length l, it has a prefix of length l-1 that is the bit string representation of its parent.
- as an ordered pair, x=(l,n), the parent is the pair (l-1,m) where m = floor(n / 2).
When the hierarchy doesn’t need to be explicit, we can use a simplified definition of Xk
[]
The functions minBL(n) and toBitString(l,n) are also expressed in Javascript at appendix.
All above definitions also apply to the term “Sized Integers” used in some implementations. As in usual generalizations from ℕ to ℤ, can be accomplished with some control and carrying the sign.
Hierarchy as nested set collection
A nested set is a set containing a chain of subsets, forming a hierarchical structure. In Set Theory it is related to partial order, and nested sets are used as reference for any hierarchy or class inheritance definitions.
Let B be a non-empty set and C be a collection of subsets of B. Then C is a nested set collection if:
[] So we can suppose that the collection C that represent the k-Natural Codes hierarchy is defined by Ck = {X1, X2, ..., Xk} = { P1, P1∪P2 , ..., P1∪P2∪ ... ∪Pk} where the union operations are demonstrating that the second condition is satisfied. So always is true that X1 ⊂ X2 ⊂ X3 ⊂... ⊂ Xk and that the collection Ck is a partial order for “⊂”, so a strict containment order. In other words, we can say that X3 is the parent of X2 that is the parent of X1. The index i convention ensures that i<a imply Xi⊂Xa .
The hierarchy of the elements, most important and commented before, can be expressed by the relations between prefixes of the elements of a set Xi and its parent Xi-1. Every element x of Xi with more than one bit,
- the bit string representation is a concatenation of a prefix p and a suffix s, x=p⊕s, where p ∈ Xi-1 .
- in the pair representation x=(l,n) and p=(l-1, floor(n / 2)) ∈ Xi-1
Hidden bit representation
The hidden bit strategy is consistent (see also practical implementations). There is a bijective relation f: Xk → Hk⊂ℕ and its inverse f -1 that maps any Natural Code into a natural number,
f(l,n) = n+2l f -1(m) = [minBL(m)-1 , m-2minBL(m)].
The function f adds one bit to the value, and f -1 removes it. When Natural Code is expressed by bit strings i of the set Pk the function produces the set P’k of numbers, and can be expressed as
f(i) = cast_to_integer( bitwise_or(i,2^k) ).
The construction of Hk follows the recurrence rule, Hk = P’k ∪ Hk-1.
In programming languages we can promote an entity to first-class citizen when it supports all the operations generally available to other primitive entities. That is the case, the elements of Hk are primitive (e.g. Bigint data type), and any integer function can be used — e.g. integer comparizon to check equals, or specialized m_compare_lexOrder(a,b) of the appendix to sort, or any bitwise function to extract prefixes. The main application is to use it as a 64 bits primary key in a database.
Bit string and base2h notation
In this article, to represent bit string values without ambiguity, we adopted the base-subscript notation with “2h” standing “hierarchical base2”. Examples: [011]2h , [000]2h ≠ [00]2h.
Similarly a sequence can be expressed in brackets. For instance, the elements of X2 in lexicographic order can be expressed by a sequence: S2=[0, 00, 01, 1, 10, 11]2h.
Strictly speaking, it is not valid to compare a Natural with a SizedNatural, except when casting datatypes. Example: toBase2([00]2h) = [0]2. For internal representations (hidden bit) it is necessary to assign equivalence, for example to say that [00]2h is internally mapped to [100]2.
Lexicographic and numeric orderings
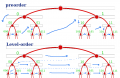
An ordering is a method for sorting elements, and it can be based on a comparison algorithm or conversion to a natural number. Mathematically the Natural Code set Xk is an well-order set when every non-empty subset of Xk has a least element (by the chosen comparison). For practical applications there are two main alternatives:[]
- binary lexicographic order: the bit “0” is the least in the set
{0,1}, that is the alphabet of the bit string. The same result in a
binary tree, the Cantor Set labeled by Natural Codes, listing codes
during traverse, is known as preorder (illustrated).
Note: in computers the direct bit string comparison is the faster
algorithm (scan and compare each bit), but when using pair
representation, other algorithms can be used to avoid casting (see
appendix).
- numeric level order: is the “natural order” of the numeric
(right-copy) hidden bit representation. The level order in a binary tree (illustrated) is known by the same name. Example using X2 in a bit string representation but numeric level order sequence, S’2=[0, 1, 00, 01, 10, 11]2h. When using the pair representation, (l,n), the algorithm to compare a and b is: if (a.l≠b.l) them a.l<b.l else a.n≤b.n.
For hidden-bit internal representation is possible to implement lexicographic order without bit string convertions. The algorithm is based into a function that count the leading zeros, prefix_length(x), and can be expressed by a non-recursive algorithm. The sort method calls a compare(a,b) function that returns a boolean, false if a is “less” than b, null if they are “equal”, and true if the a is “greater”. In the appendix we demonstrate that the function exists (see m_compare_lexOrder) and eventually can be optimized in low-level implementations (in C or assembler languages), to be faster than the “cast to bit string”.
Positional representation of Natural Codes
Natural numbers can be expressed with positional notation, using the rule of "remove leading zeros". The rule is used in any base (radix) representation. The Natural Code's representation is like “natural numbers without the rule of remove leading zeros”, and not affects prefix hierarchy in any of its valid base representation. The solution to accomplish forbidden conversions will be explained in the next subsections: as illustrated in Table-2, is to extend base4 and base16 alphabets, adding a last digit when forbidden, a digit with new symbols (examples in bold below).
Table 2 +-----------------------------------+-----------------------------------+ | (size,value) BitString | (size,value) BitString | | Base4h Base16h | Base4h Base16h | | (1,0) | (1,1) | | 0 | 1 | | G G | Q Q | | (2,0) | (2,2) | | 00 | 10 | | 0 H | 2 R | | (3,0) | (3,4) | | 000 | 100 | | 0G J | 2G S | | (4,0) | (4,8) | | 0000 | 1000 | | 00 0 | 20 8 | | (4,1) | (4,9) | | 0001 | 1001 | | 01 1 | 21 9 | | (3,1) | (3,5) | | 001 | 101 | | 0Q K | 2Q T | | (4,2) | (4,10) | | 0010 | 1010 | | 02 2 | 22 a | | (4,3) | (4,11) | | 0011 | 1011 | | 03 3 | 23 b | | (2,1) | (2,3) | | 01 | 11 | | 1 M | 3 V | | (3,2) | (3,6) | | 010 | 110 | | 1G N | 3G Z | | (4,4) | (4,12) | | 0100 | 1100 | | 10 4 | 30 c | | (4,5) | (4,13) | | 0101 | 1101 | | 11 5 | 31 d | | (3,3) | (3,7) | | 011 | 111 | | 1Q P | 3Q Y | | (4,6) | (4,14) | | 0110 | 1110 | | 12 6 | 32 e | | (4,7) | (4,15) | | 0111 | 1111 | | 13 7 | 33 f | +-----------------------------------+-----------------------------------+ | ... ... ... | ... ... | | ... | ... ... | | (8,29) | (10,117) | | ... 0131 1d | | | (9,58) | ... 01311 | | | 1dH | | ... 0131G | (9,59) | | 1dG | | | (10,116) | ... 0131H | | | 1dQ | | ... 01310 | (10,118) | | 1dH | | | | ... 01312 | | | 1dR | +-----------------------------------+-----------------------------------+
The column Base4h on Table 2 shows that there is prefix preservation, ensuring that hierarchical subsets can be obtained by simple syntax inspection. The elements of the illustrated subset of the green apples, G, subset of the set A of apples, can be selected by the prefix “1”.[]
A = {“G“, “0“, “0G“, “1“, “1G“, “1Q“} G = {“1“, “1G“, “1Q“} ⊂ A
Bit string or base2h
The bit string representation is the simplest and the canonic one. The Natural Code bit string representation is the base2h: the ordinary base2 augmented with the "use leading zeros" rule (00 and 0 are distinct elements).
Base4h
How to convert one-digit bit strings 0 and 1 to base4? Or the bit strings like 000? The translations [00]2h=[0]4 and [01]2h=[1]4 make sense for bit strings, but there are no standard rule or tradition for translate 1 bit, 3 bits, 5 bits etc. bit strings. [0]2h=[?]4 ; [1]2h=[?]4 ; [000]2h=[?]4.
[]
The solution is to use a fake digit that represent these values. To avoid confusion with hexadecimal letters we can use G to represent 0 and Q to represent 1. It is named “non-hierarchical digit” (nhDigit), because, despite accommodating hierarchical representation, it is not a member of the hierarchy. The “base4 extended for hierarchy” was shortened to “base4h”. Table-2 is illustrating base4h representation of all elements of the X4 set.
Base4h numbers are strings with usual base4 pattern and the nhDigit as optional suffix. This syntax rule, to recognize arbitrary base4h codes, can be expressed by a regular expression:
/^([0123]*)([GQ]?)$/
The inverse, to translate from bit string with b bits, when b is even we can use ordinary base4 conversion, and when b is odd, concatenate the nhDigit. Splitting (e.g. with Javascript) the binary value as prefix and suffix parts,
let part = bitString.match(/^((?:[01]{2,2})*)([01]*)$/)
the prefix (part[0]) will be translated to usual base4 number, and the suffix (part[1]), when it exists (a remaining last bit) will be translated to nhDigit by this JSON map: {"0":"G","1":"Q"}. []
Example: to convert 001010010 into base4h, split into parts, part[0]=00101001 of 2-bits blocks from begin, that will result in “0221”, and part[1]=0, of remaining bit, resulting in “G”. Concatenating part results, “0221G”.
Base16h
This encoding extension for base16 (RFC 4648, sec 8) was inspired in the base4h encode. It uses the same nhDigit concept: a complementary syntax to ordinary base representation where the last digit can use an alternative alphabet to represent partial values (with less bits) of ordinary digits.
We can use hexadecimal representation for any integer, but when controlling the bit-length can use only base16-compatible lengths: 4 bits, 8 bits, 12 bits, ... multiples of 4. So, how to transform into base16 the bit strings like 0, 1, 00, 01, 10, ... ?
The solution is to extend a hexadecimal representation, in a similar way to the previous one used for base4h: the last digit as a fake-digit that can represent all these incompatible values — so using the nhDigit values G and Q for 1-bit values, and including more values for 2 bits (4 values) and 3 bits (8 values). The total is 2+4+8=14 values, they can be represented by the letters G to T or any other set of 14 letters — table 3 shows our choices.
The set was optimized excluding vowels (I,O,U) and symbols that may be easily confused with each other (as L), and excluding X because is used as hexadecimal convertion prefix (e.g. x0123).
The name of this new representation is base16h, because it is the “ordinary base16 extended for hierarchy”:
/^([0-9a-f]*)([GHJKMNP-TVZY])?$/
The inverse, to translate from bit string with b bits, there are b%4 last bits to be translated to a nhDigit. Splitting (e.g. with Javascript) the value as prefix and suffix parts,
let part = bitString.match(/^((?:[01]{4,4})*)([01]*)$/)
the prefix (part[0]) will be translated to usual hexadecimal number, and the suffix (part[1]), when exists (with 1, 2 or 3 last bits), will be translated by this "last bits to nhDigit" JSON map:
{ "0":"G", "00":"H", "000":"J", "001":"K", "01":"M", "010":"N", "011":"P", "1":"Q", "10":"R", "100":"S", "101":"T", "11":"V", "110":"Z", "111":"Y"
}
Example: to convert 0010100101 into base16h, split into part[0]=00101001 of 4-bits blocks from begin, and part[1]=01, of remaining bits. Convert part[0] into ordinary hexadecimal (00101001 is “29”), and part[1] by the JSON table above (01 is “M”), so it results in “29M”.
Base8h
This encoding is less usual, but use the same pattern and implementation tham base16h.
String-detection pattern: /^([0-7]*)([GQHMRV])?$/ Split into parts: bitString.match(/^((?:[01]{3,3})*)([01]*)$/) JSON map for nhDigit: { "0":"G", "00":"H", "01":"M", "1":"Q", "10":"R", "11":"V" }
Example: to convert bit string 0010100101 into base8h, split into part[0]=001010010 of 3-bits blocks from begin, and part[1]=1, of remaining bits. Convert part[0] into ordinary octal (001010010 is “122”), and part[1] by the JSON table above (1 is “Q”), so it results in “122Q”.
The Natural Code algebra
The base4h, base8h and base16h representations are compact expressions of the bit string representation, and all can be converted to each other without restrictions. Examples of functions and operations:
- Formal group algebra: as demonstred before, the set of Natural Codes
can be generalized with the “+” operator and “∅” as identity element, forming a cyclic group.
- Complementar operations: prefix remove, prefix concatenation and
other practical operations are valid in bit string and base-h representations — provided that a suffix of sufficient length for the base-h last digit.
- Positional representation: any code x of the set of all Natural
Codes can be represented as bit string or a “base nh” with n in
{2,4,8,16}. There is a function encode_baseh(x,n) that returns an
human-readable expression s for x, using an alphabet of n symbols,
and its inverse decode_baseh(s,n) that returns x.
Also, there is a kind of encode/decode algebra for cast operations
over internal 64 bits representation.
- Order by different criteria. The bit string ascending order is
defulat, but descending, or level-order, or binary-tree traversals orders, etc. are also valid.
Base-h order and collation
To simplify base-h, we reuse alphabets: alphabet(base4h) ⊂ alphabet(base8h) ⊂ alphabet(base16h).
Another important decision, to keep the standard numerical representations as a subset of base-h: base4 ⊂ base4h; base8 ⊂ base8h; base16 ⊂ base16h.
We pay a high price for the last decision when we are ordering a list of codes: "base16 numeric order" and "base16h bitstring order" are interleaved. The aim is the bit string lexicographical order, as in the table beside, where the colored cells show the interleaving problem.
The best that we can do, for human-reader, is to preserve order in the set of hexadecimal digits, and the order in the set nhDigits. The complete (union of sets) order must use, for example, a translation in the code’s last digit.
Assuming a column x of natural codes in base16h, in a SQL database. The “ORDER BY x” will fail. It needs a character translation, here expressed in PostgreSQL:
SELECT x FROM t ORDER BY traslate( x, 'GHJ01K23MN45R67QRS89TabVZcdYef', '0123456789ABCDEFGHIJKLMNOPQRST' ) -- or only last-digit translation
To be friendly, avoiding translations, the base-h codes must be represented by text with special collation. Supposing that base-h will be a standard, it is natural to propose a collantion for it. Imagine defining a column as base16h representation:
CREATE TABLE t (x text COLLATE "num_b16h");
Base 32rh and others
The number of human-readable new digits in the nhDigit alphabet (and the ability of remember its order) is limited. In this article we recommend limiting it to the base 16h.
Any other base b representaion preserving hierarchy is possible by leading zeros and usual restriction to convert bit strings with restricted sizes, the multiples of log2(b) bits, illustrated before in Table-1. To avoid confusion with the ordinary base conversion, we adopt the terminology “base b with restricted hiearchy”. For exemple “base 32 with restricted hiearchy”, or short “base32rh” — it is not “base32” because use leading zeros and it is not “base32h” because it can't be used perfectly in an algebra of Natural Codes.
For exemple Geohash codes “6g” and “6g55” are base32rh representations, and can be converted to hexadecimal (base16) representation, but “6” and “6g5” can’t. Codes with an odd number of digits are not convertible (only to base16h instead base16).
NOTE. The same definition is not so useful but is also valid also for base4rh, base8rh and base16rh. That said, it should be remembered that, strictly speaking, ordinary base conversion does not apply to bit strings due to the loss of information. We must use only “h” and “rh” bases for bit string representation.
Algorithms
There are many ways to store internally a Natural Code of our formal definition. The choice is a matter of context (e.g. database or interface), simplicity and language. Main options for internal representation:
s bit string. Two ways:
- bits: real buffer of bits. Example: bit varying datatype of
PostgreSQL. Best case.
- characters: using the ASCII characters “0” and “1”, in a text
string. Worst case.
(l,n) length and value. Small integer for l and “big integer” for n. Used in formal definition.
(p,n) padded zeros and value. Small integer for p and “big integer” for n. Not used.
m only a value, using the hidden-bit strategy. The same “big integer” n, but m is unsigned, and internally uses more one bit to protect leading zeros.
Any of these options can be optimized when values are limited to, e.g. 32 or 64 bits.
All algorithms and conventions presented in this article were tested using Javascript, using Web context constraints and performance evaluations. The SizedNatural concept was adapted to the Javascript primitive type BigInt. We also implemented SizedNatural concept in PostgreSQL database, using the hidden bit strategy. In a future release we will develop C++ code to run as database library or WebAssembly Javascript object.
Bit strings into integers
Finite natural numbers are represented in computers by unsigned integers of fixed length, typically 64 bits (8 bytes), and eventually by a variable-length in arbitrary-precision arithmetic frameworks. For simplicity, many databases and programming languages do not offer unsigned, only signed integers. Therefore, to use the hidden bit strategy is necessary to adapt the bit string to regular integers.
There are no IEEE standards, but the "standard" internal representation for regular integers is the following:
- positive values, like unsigned integers, are represented from left
to right, ending with the unit (less significative bit) in the right.
- the signal is the first (leftmost) bit. Zero is positive and 1 is
negative.
- negative values are represented as "two's complement". When signal
changes, all numeric representation also changes.
The hidden bit representation with regular integers depends on the implementation context. The conversion from bit string to integer, in order to be optimized, it must be specified as a whole. The first decision is the copy, related with the two different internal representations, the left_copy and and right_copy:
+-----------------------+-----------------------+-----------------------+ | original | left_copy | right_copy | +-----------------------+-----------------------+-----------------------+ | 011100 | [0011100100000 | [0000000000000 | | | 0000000000000000000]2 | 0000000000001011100]2 | | | | = [92]10 | | | = [956301312]10 | | +-----------------------+-----------------------+-----------------------+
In PostgreSQL it can be performed by this query:
SELECT *, left_copy::int, right_copy::int FROM ( SELECT x AS original, (b'0' || x || b'1')::bit(32) AS left_copy, overlay( b'0'::bit(32) PLACING (b'01'||x) FROM 31-length(x) ) AS right_copy FROM (select b'011100') t(x) ) t2; -- any bitstring with less than 31 bits
In order to preserve original variable-size information into the fixed-size representation: the left copy must be protected on the right, and the right copy on the left. For ordering and for human intuition the best is to use right_copy. Some systems, like S2 Geometry, use the left_copy, and has some rationale for it: it is easy and fast to get a fix-lenght hierarchical prefix, the most frequently used operation. Anyway left_copy doesn't follow the lexicographical order.
On arbitrary precision integers, a candidate to variable-length representation, is rare to implement it directly as BitArray, they are optimized for CPU word (e.g. of 8, 32 or 64 bits) and big-endian/little-endian representations.
The main context-algorithm choices are summarized in the table below. Notation: x is the bit string, s is the signal ‘0’ bit, h the ‘1’ left-mark for hidden bit right_copy, k the ‘1’ right-mark for hidden bit left_copy. The symbol “⊕” is the concatenation operator.
----------------------------------- ------------------------------ ------------------------------------- Context Loss of bits (n:description) Algorithm’s label and spec. summary Arbitrary precision, unsigned int 1: h A1: Concatenation h⊕x and cast. Arbitrary precision, signed int 2: s and h A2: s⊕h⊕x and cast. Fixed length, unsigned int8 1: h A3R: h⊕x and cast to right. Fixed length, unsigned int8 1: k A3L: x⊕k and cast to left. Fixed length, int8 2: s and h A4R: s⊕h⊕x and cast to right. Fixed length, int8 2: s and k A4L: s⊕x⊕k and cast to left. ----------------------------------- ------------------------------ -------------------------------------
NOTES: 1. the optimized implementation is not the specification. In C-language for example we can use the union datatype and copy directly the bit string into adequate position. 2. the (signed) integer algorithms not use the signal bit to avoid complexity. 3. In this article we are limited to discussion of the tested implementations, for Javascript (algorithm A2) and PostgreSQL (algorithm A4L).
Examples:
-------- -------------------------------------- -------------------------------------- --------------------------- ----------------------------- algor. enc( [0 ]2h) = enc( [00 ]2h) = enc( [1 ]2h) = enc( [001 ]2h) = A1 [10]2h = [2]10 [100]2h = [4]10 [11]2h = [3]10 [1001]2h = [9]10 A2 [010]2h = [+2]10 [0100]2h = [+4]10 [011]2h = [+3]10 [01001]2h = [+9]10 A3R [0…010]2h = [2]10 [0…0100]2h = [4]10 [0…011]2h = [2]10 [0…01001]2h = [9]10 A3L [010…0]2h = [4611686018427387904]10 [0010…0]2h = [2305843009213693952]10 [110…0]2h = [1383…3712]10 [00110…0]2h = [3458…0928]10 A4R [00…010]2h = [+2]10 [00…0100]2h = [+4]10 [00…011]2h = [+3]10 [00…01001]2h = [+9]10 A4L [010…0]2h = [2305843009213693952]10 [0010…0]2h = [1152921504606846976]10 [110…0]2h = [6917…1856]10 [00110…0]2h = [1729…0464]10 -------- -------------------------------------- -------------------------------------- --------------------------- -----------------------------
The internal representation of algorithm A4L is illustrated below.
Signed implementation
Illustrating the left_copy case.
Javascript only has the option to represent larger natural numbers through the native Bigint datatype. The best algorithm for this context is algorithm A2. Two bits are lost, with 62 bits remaining to be used as Natural Code. The appendix contains Javascript implementations.
Int8 implementation
PostgreSQL offers direct bit string representation (named varbit) and int8 (named bigint). The conversion from varbit to bigint is easy with both algorithms, A4R and A4L. Using the same examples, to reproduce the four columns of the table, the SQL statement is:
SELECT 'A4R' alg, b'10'::bigint x0, b'100'::bigint x1, b'11'::bigint x2, b'1001'::bigint x3 UNION SELECT 'A4L', b'0010000000000000000000000000000000000000000000000000000000000000'::bigint, b'0001000000000000000000000000000000000000000000000000000000000000'::bigint, b'0110000000000000000000000000000000000000000000000000000000000000'::bigint, b'0001100000000000000000000000000000000000000000000000000000000000'::bigint ;
The generic functions, taking the original bit string x as input, use
varbit_to_bigint(b'01'||x) for algorithm A4R and
(b'0'||x||b'1')::bit(64)::bigint for algorithm A4L. Two bits are lost,
62 bits are left to store the Natural Code x.
To get back the bit string, it is possible to use substring bit string operations to remove the extra bit with knowledge of its position. In the case of algorithm A4R, the position can be obtained from integer base2-logarithm. In the case of algorithm A4L, the “right-most non-zero bit position” needs a specialized function that is non-optimized, except by implementing with C-language, using the CLZ function.
Comparing Natural Codes
There no constraint in our Natural Code definition about order, any one is valid. We adopted the bit string lexicographic order as canonic (see the line sequence at tables 1 and 2), that corresponds, in the Complete Binary Tree models, to the pre-order traversal. See functions _compare_lexOrder(a,b) at appendix. It is canonic because in a listing it groups same-prefix items. The most simple, pair_compare_lexOrder(a,b) uses pair_toBitString(l,n) for basic string comparison. For best performance the ideal internal representation is m (hidden bit), that is direct numeric comparison — can be tested with m_compare_lexOrder(a,b).
The library offers also the level-order. The m_compare_levelOrder(a,b) function it is an integer comparison. The pair_compare_levelOrder(a,b) function is implemented by l and n numerical comparisons: when a.l=b.l it compares a.n and b.n.
Trucating
The most usual is to truncate a prefix, see _truncate(x,bits) function at appendix. Sometimes it is useful to split a Natural Code into both a prefix and suffix for a new Natural Code.
Base conversion
Mathematical libraries, like the native Javascript BigInt, have good performance in ordinary base conversion (see BigInt.toString(radix) method). The most frequently used ones are 4, 8,16, 32 and 64. The alphabet can be controlled by some standardization, see example in the appendix. The base4h and base16h, as shown above, have additional performance cost to split the bit string into prefix (that use fast native conversion of ordinary base) and nhDigit, that is a fast key-value conversion.
Tested implementations
To test concepts of the article and algorithms described above, we implemented them in two flavors: Javascript and SQL. It is pending a complementary C++ library to offer optimized versions of critical critical functions, like the integer logarithm and the CLZ funcion, or perhaps also base conversion functions.
All implementations were done with Apache v2.0 license and can be accessed at git.osm.codes.
Javascript SizedBigInt
Sized BigInt's are arbitrary-precision integers adapted to represent Natural Codes. It is a Javascript class, using primitive data type BigInt in internal representation. The class also was extended to represent discrete global grid cell identifiers, like Geohash, and its encoding options.
See also Krauss (2019) with online demonstration of labeling quadrilateral grid cells of Space-filling curves.
SQL NatCod
We also implemented Natural Codes concept in PostgreSQL database, using bit strings (the bit varying datatype), and optional hidden bit strategy for usual fixed 64 bits integers (the bigint datatype of the database). The bigint is useful for indexes and internal operations, and some cases of intermediary data interchange.
Terminology
Base: the web standards, as RFC 4648, use the term "base", but Javascript (ECMA-262) adopted the term "radix" in parseInt(string,radix). The preferred term is base.
Base alphabet: is the "encoding alphabet", a set of UTF-8 symbols used as digit values of a specific base.
Base label: each pair (base,alphabet) need a short label. In the SizedBigInt class some labels was defined: base2, base4, base4h, base8, base16, base16h, base32, base32ghs, base32hex, base32pt, base32rfc, base64, base64url, base64rfc. See also the ID column of the catalog-base.csv file at class’ git repository.
Default alphabet: is the alphabet adopted as standard for a specific base, associated with the label "baseX", for example "base4" is a synonym for "base4js", the ECMA-262 standard for it. See base label.
Padding: SizedBigInt's are numbers where padding zeros make difference (0 is not equal to 00). The RFC 4648 is not for numbers, the convention of pad "=" characters at the end of encoded data was adopted.
Set, element, number, natural number and Integer are terms of the Set theory (Halmos 1960), the formal mathematical foundation used here. In implementation context the Javascript semantic for integer, class, number, etc. is preferred.
Size and length: the term "size" was used in the title of this project, but the usual term for "size of the string" is length and, for binary numbers, bit-length, the preferred term.
Sized BigInt: term used in the first Javascript library for Natural Codes, where the term BigInt is used to express arbitrary-leght integer numbers.
Sized Integer: the formal definition expressed in this article is about natural numbers (positive Integers), but it is easy to generalize, this was only a simplification in order to avoid signal analysis and to reuse implementations.
Unsigned Sized Integer: synonym for Natural Code. In Computation the term “unsigned integer” is preferred in place of “natural number”.
References
Standards:
ECMA-262 v9.0 (2018), “ECMAScript® 2018 Language Specification”.
ISO 80000-2:2009, "Quantities and units—Part 2: Mathematical signs and symbols to be used in the natural sciences and technology", Chapters 5 and 6.
RFC 4648 (2006), "The Base16, Base32, and Base64 Data Encodings".
Other works:
J. Ferreirós (2007), "Labyrinth of Thought, A History of Set Theory and Its Role in Modern Mathematics", Second revised edition. ISBN 978-3-7643-8349-7.
P. Halmos (1960), "Naive Set Theory". ISBN 978-1-61427-131-4.
P. Krauss, E. Bortolini, T. Jean, R. P. Julião (2018), “Geohash Generalizado: uma metodologia para a implementação de funções de hash geradoras de geocódigos hierárquicos base32, Versão 0.4”, urn:doi:10.5281/zenodo.2529558.
P. Krauss (2019), “SFC4Q Space-filling curve valid to index hierarchical grid of aperture-4 quadrilateral cells”, software source-code. urn:doi:10.5281/zenodo.7112018.
P. Krauss, Claiton (2023), “NaturalCodes Library”. https://git.osm.codes/NaturalCodes
D. R. Merlo, J. A. R. Martín-Romo, T. Alieva, M. Calvo (2003), “Fresnel Diffraction by Deterministic Fractal Gratings: An Experimental Study”, urn:doi:10.1134/1.1595227 (open).
C. E. Shannon (1948), “A Mathematical Theory of Communication”. urn:doi:10.1002/j.1538-7305.1948.tb01338.x.
L. A. Steen, J. A. Seebach (1995), “Counterexamples in Topology”. ISBN 978-0-486-68735-3.
A. M. Turing (1937), “On Computable Numbers, with an Application to the Entscheidungsproblem”. urn:doi:10.1112/plms/s2-42.1.230.
Appendix - supplementary material
The lexicographic adition and its cyclic group
As showed in this mathematical proof example, it is long and deserves a separate article for a group theory contextualization of the Natural Codes. The choice of zero have two alternatives and must be also dicussed.
Basic Natural Codes functions
These functions are used only as functional specification and didactic reference, not for optimized implementations neither offering pre-conditions or exceptions. All were done in Javascript (ES6+), and at functions, the input parameter “l” can be a “Number(l)”; input parameter “n” must be a “BigInt(n)”; input parameter “x” must be an array of size, “x[0]” and value, “x[1]”. Name prerfix “pair_” and “m_” refer representation.
Utility functions:
function minBL(n){
// calculates bigInt_log2(n)+1, the minimum bit length of BigInt n.
for(var count=0; n>BigInt(1); count++) n = n/BigInt(2)
return count+1
}
function pair_minBL(x) { return minBL(x[1]) }
function m_minBL(m) { return minBL(m)-1 }
Functions using pairs (l,n) as internal representation:
// javascript Array convention x[l,n]. So x[0] is l and x[1] is n.
function pair_toBitString(x) {
// transforms BigInt of (l,n) representation into a bit string
representation.
return x[1].toString(2).padStart(x[0],'0')
}
function pair_fromBitString(s) {
let l = s.length
let n = BigInt("0b"+s)
return [l,n]
}
function pair_truncate(x,bits) {
return pair_fromBitString( pair_toBitString(x).slice(0,bits) );
}
function pair_compare_lexOrder(a,b) {
// compare in lexical (ASCII) order the two arrays
let str_b = pair_toBitString(b)
return pair_toBitString(a).localeCompare(str_b)
// same as (str_a>str_b)? 1: ( (str_a==str_b)? 0: -1 )
}
function pair_compare_levelOrder(a,b) {
let bitsDiff = a[0] - b[0] // compare bitLengths (l)
if (bitsDiff) return bitsDiff;
else { // when equal lengths, compare BigInts (n)
let valDiff = a[1] - b[1]
return valDiff? ((valDiff>BigInt(0))? 1: -1): 0
}
}
function pair_lexOrder_next(x,maxBits=null,cycle=false) {
// the successor of x in a context of lexicographical order,
returning string
let t = x[0] // x[0] is the size, x[1] the value
if (!t) return null;
if (!maxBits) maxBits=t; else if (t>maxBits) return null;
let s = pair_toBitString(x)
if (t<maxBits) return s+'0';
t--
if (s[t]=='0') return s.slice(0,t)+'1';
else return (s==''.padEnd(maxBits,'1'))? (cycle?'0':null):
s.slice(1);
}
Functions using m of the hidden bit strategy as internal representation:
function m_toBitString(m) {
// transforms hidden_bit BigInt representation into a bit_string
representation.
return (m===null)? '': m.toString(2).slice(1)
}
function m_fromBitString(s) {
return s? BigInt("0b1"+s): null
}
function m_truncate(m,bits) { // can be optimezed
return m_fromBitString( m_toBitString(m).slice(0,bits) )
}
function m_compare_lexOrder(a,b) {
// compare two SizedBigInt of m representation
let dif;
let bdif = m_minBL(a) - m_minBL(b)
if (bdif) {
dif = (bdif>0)
? a/BigInt(2**bdif) - b // normalize a
: a - b/BigInt(2**(-bdif)); // normalize b
if (!dif) dif = bdif; // 0 before 00, 101 before 0101 etc.
} else
dif = a - b
return dif? ((dif>BigInt(0))? 1: -1): 0
}
function m_compare_levelOrder(a,b) {
let dif = a - b
return dif? ((dif>BigInt(0))? 1: -1): 0
}
Encoding alphabets and conventions
Complete list of standard alphabets for base conversion. Only “power of 2” bases. The identifier is the concatenation of word “base”, the value of the base and the alphabetLabel.
+-----------+-----------+-----------+-----------+-----------+-----------+ | base | alphabet | id | bits | alphabet | Reference | | | label | | /digit | (after | standard | | | | | | space | | | | | | | nhDigits) | | +-----------+-----------+-----------+-----------+-----------+-----------+ | 2 | js* | base2js | 1 | 01 | ECMA-262 | +-----------+-----------+-----------+-----------+-----------+-----------+ | 4 | js* | base4js | 2 | 0123 | ECMA-262 | +-----------+-----------+-----------+-----------+-----------+-----------+ | 4 | h | base4h | 2 | 0123 GQ | ECMA + | | | | | | | nhDigits | | | | | | | alphabet | +-----------+-----------+-----------+-----------+-----------+-----------+ | 8 | js* | base8js | 3 | 01234567 | ECMA-262 | +-----------+-----------+-----------+-----------+-----------+-----------+ | 8 | h | base8h | 3 | 01234567 | ECMA + | | | | | | GQ HMRV | nhDigits | | | | | | | alphabet | +-----------+-----------+-----------+-----------+-----------+-----------+ | 16 | js* | base16js | 4 | 0123456 | ECMA-262 | | | | | | 789abcdef | and RFC | | | | | | | 4648/sec8 | +-----------+-----------+-----------+-----------+-----------+-----------+ | 16 | h | base16h | 4 | 0123456 | ECMA + | | | | | | 789abcdef | nhDigits | | | | | | GQ HMRV | alphabet | | | | | | JKNPSTZY | | +-----------+-----------+-----------+-----------+-----------+-----------+ | 32 | hex* | base32hex | 5 | 01234 | ECMA-262 | | | | | | 56789abcd | and RFC | | | | | | efghijklm | 4648/sec7 | | | | | | nopqrstuv | | +-----------+-----------+-----------+-----------+-----------+-----------+ | 32 | ghs | base32ghs | 5 | 01234 | Geohash | | | | | | 56789bcde | | | | | | | fghjkmnpq | | | | | | | rstuvwxyz | | +-----------+-----------+-----------+-----------+-----------+-----------+ | 32 | nvu | base32nvu | 5 | 01234 | No-Vowels | | | | | | 56789BCDF | except U | | | | | | GHJKLMNPQ | (near | | | | | | RSTUVWXYZ | non- | | | | | | | syllabic) | +-----------+-----------+-----------+-----------+-----------+-----------+ | 32 | rfc | base32rfc | 5 | ABCDE | RFC | | | | | | FGHIJKLMN | 4648/sec6 | | | | | | OPQRSTUVW | | | | | | | XYZ234567 | | +-----------+-----------+-----------+-----------+-----------+-----------+ | 64 | url* | base64url | 6 | A | RFC | | | | | | BCDEFGHIJ | 4648/sec5 | | | | | | KLMNOPQRS | | | | | | | TUVWXYZab | | | | | | | cdefghijk | | | | | | | lmnopqrst | | | | | | | uvwxyz012 | | | | | | | 3456789-_ | | +-----------+-----------+-----------+-----------+-----------+-----------+ | 64 | rfc | base64rfc | 6 | A | RFC | | | | | | BCDEFGHIJ | 4648/sec4 | | | | | | KLMNOPQRS | | | | | | | TUVWXYZab | | | | | | | cdefghijk | | | | | | | lmnopqrst | | | | | | | uvwxyz012 | | | | | | | 3456789+/ | | +-----------+-----------+-----------+-----------+-----------+-----------+
(*) default base. For example base32 is interpreted by default as base32hex. All base32 here are using with leading zeros, they are valid instances of “restricted hiearchy”, base32rh.
[art. 1 / pag. ]
[1] OpenStreetMap Brasil Community. ✉ peter@openstreetmap.com.br or thierry@openstreetmap.com.br.
[2] Universidade Federal do ABC (UFABC) / Centro de Matemática, Computação e Cognição (CMCC).
[3] SciCrop.com
[4] Department of Geomatics, Federal University of Parana, Curitiba - PR - Brazil. ✉ evertonbertanbortolini@gmail.com
[5] Universidade Nova Lisboa, Dep. de Geografia e Planeamento Regional da NOVA FCSH, Portugal. ✉ rpj@fcsh.unl.pt
[6] GIScience Research Group, Heidelberg University, Germany.
[7] Municipality of Itanhaém, SP, Brazil.
[8] Adopting the spelling of a proper name, despite the analogy with the standard "natural numbers" (a common noun), precisely because it is not a standard.