DGGS/Cell
O principal componente do DGGS é a célula, com seu ID. Como o esquema DGGS prevê subdivisões recursivas da célula, podemos dizer que a célula dá origem à grade.
Exigência de grade regular
O padrão DGGS obriga que a forma das células não varie. Na Matemática a grade (tesselation) é um conjunto com ladrilhos (tiles), e se vai usar um tipo só de ladrilho, denomina-se a grade de regular. Já há séculos é conhecido pelos matemáticos o fato de não existirem muitas opções para se construir uma grade regular, são apenas três formatos de ladrilho:
| Forma | Vizinhanças | Subdivisão para subpavimentação | Conclusão |
|---|---|---|---|
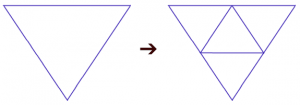
| Triangular 3 lados |
9 vizinhas (3 por aresta)
|
4 partes exatas | Pior caso de vizinhança (muitas e com apenas 25% por aresta), mas pelo menos permite a subdivisão. |
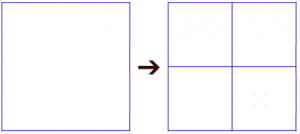
| Quadrilátero 4 lados |
8 vizinhas (4 por aresta)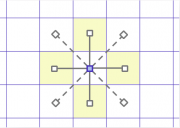
|
4 partes exatas (ou 2 retangulares) | Caso razoável de vizinhança (poucas e com 50% por aresta), subdivisão válida e flexível. |
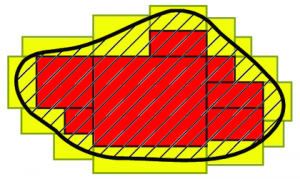
| Hexagonal 6 lados |
6 vizinhas por aresta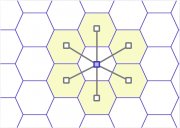
|
(impossível) | Melhor caso de vizinhança, mas impedimento no requisito da subdivisão. |
Considerações:
- Forma: é genérica. Triângulos não precisam ser equiláteros; quadriláteros podem ser losangos, paralelogramas ou retângulos.
- Adjacência: por aresta é preferível à adjacência por vértice. A adjacência refere-se não só à fronteira comum, mas também ao conjunto mais próximo de ladrilhos num raio partindo do centroide.
- Subdivisões: indicando apenas o caso de menor número, que proporcina mais niveis hierárquicos
A adjacência entre células é um importante critério na escolha de grades. Em aplicações que demandam apenas células de um só tamanho (mono-nível), tais como visualização e cálculos, principalmente em aplicações logísticas, o hexágono se sai melhor. Ele tem o menor número total de vizinhaças e todas elas por aresta (vizinhança isotrópica). Ver Uber H3. Os algoritmos hexagonais são ainda novos e um pouco mais complexos, apesar da boa performance.
Grades quadriláteras e triangulares exibem adjacência não-uniforme porque têm vizinhos de aresta e vértice (Sahr et al. 2003). As grades quadriláteras ainda assim são razoáveis, por apresentarem quantidade menor de adjacências (8 contra 12 do triângulo), com proporção maior de adjacências-por-aresta (50% contra 25% do triângulo). Todos os algoritmos conhecidos (inclusive mais complexos como FFT foram primeiramente lançados em grades quadriláteras, de modo que elas possuem amplas bibliotecas e boa performance.
Por fim, quando se fala de multifinalidade de uma grade, principalmente em aplicações cadatrais para o governo e dados públicos, é importante a capacidade de "subdivisão para subpavimentação", onde falha a grade hexagonal.
Coberturas não-hexagonais
Ladrilhos de qualquer formato e um só tamanho podem cobrir uma zona qualquer, mas uma subpavimentação requer diversos tamanhos, ou seja, ladrilhos de mais de uma grade dentro da mesma cobertura. Apenas ladrilhos triangulares e quadriláteros conseguem subpavimentar.
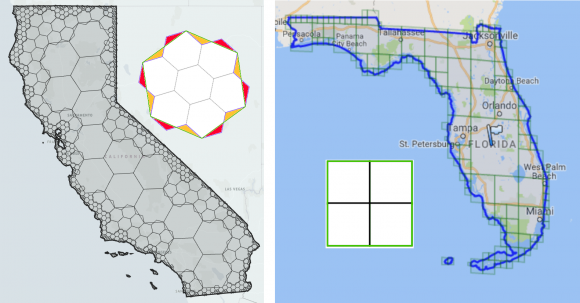
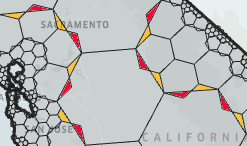
O problema dos hexágonos é melhor ilustrado abaixo, com uma subpavimentação errada e outra correta:
- INVÁLIDA: o mapa à esquerda (Califórnia) estava coberto por hexágonos de quatro tamanhos diferentes e os hexágonos se sobrepunham.
- VÁLIDA: mapa à direita (Flórida) estava coberto por formas quadriláteras (losangos) de quatro tamanhos diferentes, sem furos e sem sobreposições. Abaixo está um detalhe na Califórnia, destacando os buracos (amarelo) e as sobreposições (vermelho) entre as células maiores.
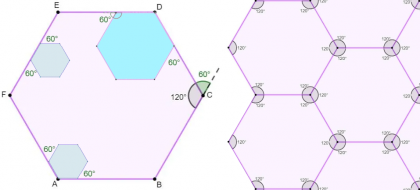
A impossibilidade de uso do hexágono para fins de subpavimentação foi demonstrada matematicamente e de forma simples por R. Israeal:
- "Em um hexágono regular, todos os ângulos medem 120 graus. Se você tiver dois hexágonos regulares de tamanhos diferentes compartilhando parte de um lado, você cria um ângulo de 180−120=60 graus. Não há como subpavimentar esse setor de 60 graus com um número finito de hexágonos regulares."